Question

Two wires, both with current out of the page, are next to one another. The wire on the left has a current of 1 A and the wire on the right has a current of 2 A. We can say that:

A. The left wire attracts the right wire and exerts twice the force as the right wire does.
B. The left wire attracts the right wire and exerts half the force as the right wire does.
C. The left wire attracts the right wire and exerts as much force as the right wire does.
D. The left wire repels the right wire and exerts twice the force as the right wire does.
E. The left wire repels the right wire and exerts half the force as the right wire does.
F. The left wire repels the right wire and exerts as much force as the right wire does.

Answer 1

C. The left wire attracts the right wire and exerts as much force as the right wire does.

Step-by-step explanation:

To know what is the answer you first take into account the magnetic field generated by each current, for a distance of d:

`B_1=(\mu_oI_1)/(2\pi d)=(\mu_o)/(2\pi d)(1A)\\\\B_2=(\mu_oI_2)/(2\pi d)=(\mu_o)/(2\pi d)(2A)=2B_1\\\\`

Next, you use the formula for the magnetic force produced by the wires:

`\vec{F_B}=I\vec{L}\ X \vec{B}`

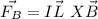
if the direction of the L vector is in +k direction, the first wire produced a magnetic field with direction +y, that is, +j and the second wire produced magnetic field with direction -y, that is, -j (this because the direction of the magnetic field is obtained by suing the right hand rule). Hence, the direction of the magnetic force on each wire, produced by the other one is:

`\vec{F_(B1)}=I_1L\hat{k}\ X\ B_2(-\hat{j})=I_1LB_2\hat{i}=(2A^2)(L\mu_o)/(2\pi d)\hat{i}\\\\\vec{F_(B2)}=I_2L\hat{k}\ X\ B_2(\hat{j})=I_2LB_1\hat{i}=-(2A^2)(L\mu_o)/(2\pi d)\hat{i}`

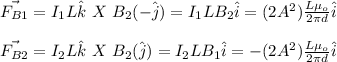
Hence, due to this result you have that:

C. The left wire attracts the right wire and exerts as much force as the right wire does.