Question

In one method of a procedure called acceptance sampling, a sample of items is randomly selected without replacement and the entire batch is accepted if every item in the sample is ok. Among 810 airport baggage scales, 102 are defective (based on data from the NY Department of Consumer Affairs). If four of the scales are randomly selected and tested, what is the probability that the entire bath will be accepted

Answer 1

`X \sim Hyp (N = 810, M=102, n=4)`

`P(X=0) = ((102C0)(810-102 C 4-0))/(810C4)`

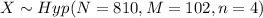
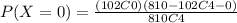
And solving we got:

`P(X=0)= ((102C0) (708C4))/(810C4) = 0.583`

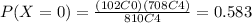
So then for the problem given the probability that the entire bath will be accepted (none is defective among the 4) is 0.583

Explanation:

For this case we can model the variable of interest with the hypergeometric distribution. And with the info given we can do this:

`X \sim Hyp (N = 810, M=102, n=4)`

`P(X=k)= ((MCk)(N-M C n-k))/(NCn)`

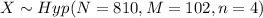
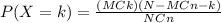
Where N is the population size, M is the number of success states in the population, n is the number of draws, k is the number of observed successes

And for this case we want to find the probability that none of the scales selected would be defective so we want to find this:

`P(X=0)`

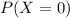
And using the probability mass function we got:

`P(X=0) = ((102C0)(810-102 C 4-0))/(810C4)`

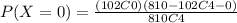
And solving we got:

`P(X=0)= ((102C0) (708C4))/(810C4) = 0.583`

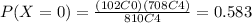
So then for the problem given the probability that the entire bath will be accepted (none is defective among the 4) is 0.583