Question

A sphere and a cylinder have the same radius and height. The volume of the cylinder is 30 m

hl
What is the volume of the sphere?
10 m
20 m
30

Answer 1

The volume of the sphere is 20 m

Explanation:

Given

Solid Shapes: Cylinder and Sphere

Volume of the cylinder
`= 30m^3`

Required

Volume of the sphere

First, we need to calculate the radius of the cylinder

The formula goes thus

`V = \pi r^2h`

By substituting 30 for V, we have

`30 = \pi r^2h`

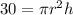
Divide through by h

`(30)/(h) = (\pi r^2h)/(h)`

`(30)/(h) = \pi r^2`

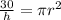
Calculating the volume of the sphere

The formula goes thus

`V = (4)/(3)\pi r^3`

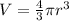
Expand Expression

`V = (4)/(3) * \pi r^2 * r`

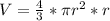
Substitute
`(30)/(h) = \pi r^2`

`V = (4)/(3) * (30)/(h) * r`

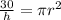
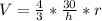
Simplify Expression

`V = (4)/(1) * (10)/(h) * r`

`V = (40)/(h) * r`

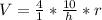
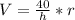
Given that the height of the cylinder and the sphere are equal

This means that the height of the cylinder equals the diameter of the sphere.

Mathematically; This is represented by

h = D

Where D represents diameter of the sphere

Recall that D = 2r (2 * radius)

Substitute 2r for D

h = 2r

Substitute h = 2r in
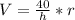`V = (40)/(h) * r`; This gives

`V = (40)/(2r) * r`

`V = (40r)/(2r)`

`V = 20`

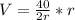
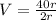
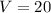
Hence, the volume of the sphere is 20 m