Answer:
a)5.88J
b)-5.88J
c)0.78m
d)0.24m
Step-by-step explanation:
a) W by the block on spring is given by
W=
 kx² =
kx² =
 (530)(0.149)² = 5.88 J
(530)(0.149)² = 5.88 J
b) Workdone by the spring = - Workdone by the block = -5.88J
c) Taking x = 0 at the contact point we have U top = U bottom
So, mg
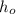 =
=
 kx² - mgx
kx² - mgx
And,
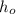 = (
= (
 kx² - mgx )/(mg) =
kx² - mgx )/(mg) =
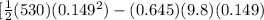 ]/(0.645x9.8)
]/(0.645x9.8)
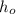 = 0.78m
= 0.78m
d) Now, if the initial initial height of block is 3
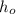
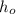 = 3 x 0.78 = 2.34m
= 3 x 0.78 = 2.34m
then,
 kx² - mgx - mg
kx² - mgx - mg
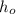 =0
=0
 (530)x² - [(0.645)(9.8)x] - [(0.645)(9.8)(2.34) = 0
(530)x² - [(0.645)(9.8)x] - [(0.645)(9.8)(2.34) = 0
265x² - 6.321x - 14.8 = 0
a=265
b=-6.321
c=-14.8
By using quadratic eq. formula, we'll have the roots
x= 0.24 or x=-0.225
Considering only positive root:
x= 0.24m (maximum compression of the spring)