Question

A​ keyboarder's speed over a 6​-min interval is given by the following​ function, where W(t) is the​ speed, in words per​ minute, at time t.

W(t) = - 5 t^2 + 20 t + 60 ​
a) Find the speed at the beginning of the interval. ​
b) Find the maximum speed and when it occurs. ​
c) Find the average speed over the 6​-min interval.

Answer 1

a) The speed at the beggining of the interval is 60 words per minute.

b) The maximum speed is 80 words per minute at the instant t = 2 minutes.

c) The average speed over the 6​-min interval is 60 words per minute.

Explanation:

a) Find the speed at the beginning of the interval. ​

This is W(0)

`W(t) = -5t^(2) + 20t + 60`

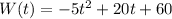
Then

`W(0) = -5(0)^(2) + 20(0) + 60 = 60`

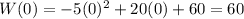
The speed at the beggining of the interval is 60 words per minute.

b) Find the maximum speed and when it occurs. ​

Suppose we have a quadratic equation in the following format:

`f(t) = at^(2) + bt + c`

The vertex is the point

`(t_(v), y(t_(v))`

In which

`t_(v) = -(b)/(2a)`

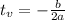
In this question:

`W(t) = -5t^(2) + 20t + 60`

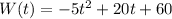
So

`a = -5, b = 20, c = 60`

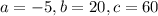
Then

`t_(v) = -(20)/(2*(-5)) = 2`

`W(2) = -5(2)^(2) + 20(2) + 60 = 80`

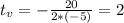
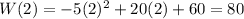
The maximum speed is 80 words per minute at the instant t = 2 minutes.

c) Find the average speed over the 6​-min interval.

The average value of a function f(x) over an interval [a,b] is:

`A = (1)/(b-a)\int\limits^b_a {x} \, dx`

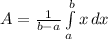
In this question:

`A = (1)/(6-0)\int\limits^6_0 {W(t)} \, dt`

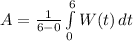
So

`F(t) = \int {W(t)} \, dt`

`A = (F(6) - F(0))/(6)`

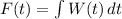
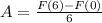
So

`F(t) = \int {-5t^(2) + 20t + 60} \, dt`

`F(t) = -(5t^(3))/(3) + 10t^(2) + 60t`

`F(6) =  -(5*6^(3))/(3) + 10*6^(2) + 60*6 = 360`

`F(0) =  -(5*6^(0))/(3) + 10*0^(2) + 60*0 = 0`

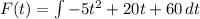
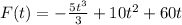
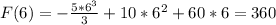
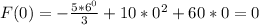
Then

`A = (F(6) - F(0))/(6) = (360 - 0)/(6) = 60`

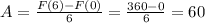
The average speed over the 6​-min interval is 60 words per minute.