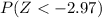Answer:
a)
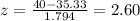
b)
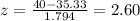
c)
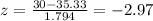
Explanation:
For this case we know that the mean for the random variable of interest is
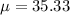 and the variance
and the variance
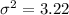 so then the deviation would be
so then the deviation would be
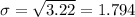
The z score is given by thsi formula:
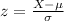
Part a
We want this probability:
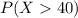
And if we find the z score we got:
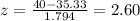
And we can find this probability:
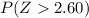
Part b
We want this probability:
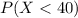
And if we find the z score we got:
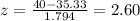
And we can find this probability:
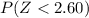
Part c
We want this probability:
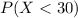
And if we find the z score we got:
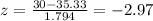
And we can find this probability: