Answer:
a)
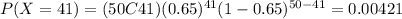
b)
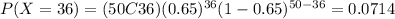
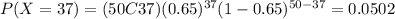
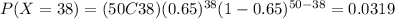
And adding these values we got:
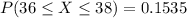
c) We can find the expected value given by:
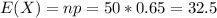
And the standard deviation would be:
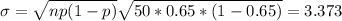
We can use the approximation to the normal distribution and we have at leat 95% of the data within 2 deviations from the mean. And the lower limit for this case would be:
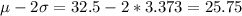
And then we can consider a value of 18 as unusual lower for this case.
Explanation:
Let X the random variable of interest "number cleared by arrest or exceptional", on this case we can model this variable with this distribution:
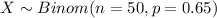
The probability mass function for the Binomial distribution is given as:
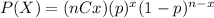
Where (nCx) means combinatory and it's given by this formula:
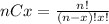
Part a
We want this probability:
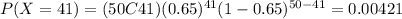
Part b
We want this probability:
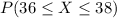
We can find the individual probabilities:
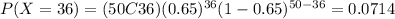
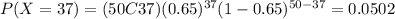
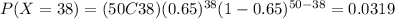
And adding these values we got:
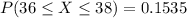
Part c
We can find the expected value given by:
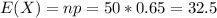
And the standard deviation would be:
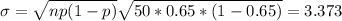
We can use the approximation to the normal distribution and we have at leat 95% of the data within 2 deviations from the mean. And the lower limit for this case would be:
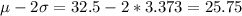
And then we can consider a value of 18 as unusual lower for this case.