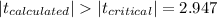Question

In the past, the mean age of consumers of a product was 37 years. Recently the product has been drastically changed. In order to determine whether there has been a change in the mean age of the product consumers, a sample of 16 consumers is selected. The mean age in the sample is 31 years and the standard deviation in the sample is 10 years. Let μ = the mean age of the current product consumers.

At a 1% significance level, the null hypothesis is rejected if:_________.

Answer 1

`t=(31-37)/((10)/(√(16)))=-2.4`

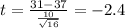
The degree of freedom are:

`df=n-1=16-1=15`

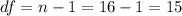
We can calculate the critical value for this case with the degrees of freedom ,we can find a critical value in the t distribution with 15 degrees of freedom who accumulate 0.005 of the area on each tail of the distribution and we got:

`t_(crit)=\pm 2.947`

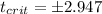
And we will reject the null hypothesis is the statistic for this case satisfy this condition:

`|t_(calculated)| > |t_(critical)|= 2.947`

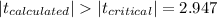
Explanation:

Information given

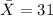`\bar X=31` represent the sample mean

`s=10` represent the sample standard deviation

`n=16` sample size

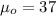`\mu_o =37` represent the value to verify

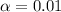`\alpha=0.01` represent the significance level

t would represent the statistic

`p_v` represent the p value for the test

System of hypotheis

We want to verify if the actual mean age of consumers of a product was 37 years and the system of hypothesis are:

Null hypothesis:
`\mu = 37`

Alternative hypothesis:
`\mu \\eq 37`

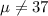
We can use the following statistic for this case:

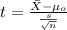`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

Replacing the info given we got:

`t=(31-37)/((10)/(√(16)))=-2.4`

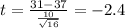
The degree of freedom are:

`df=n-1=16-1=15`

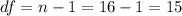
We can calculate the critical value for this case with the degrees of freedom we can find a critical value in the t distribution with 15 degrees of freedom who accumulate 0.005 of the area on each tail of the distribution and we got:

`t_(crit)=\pm 2.947`

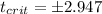
And we will reject the null hypothesis is the statistic for this case satisfy this condition:

`|t_(calculated)| > |t_(critical)|= 2.947`