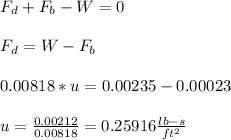Question

1. Deri had a large tank of oil (s-0.8) and was requested to determine the viscosity of that fluid. To assist with the process, she was given a 0.25-inch-diameter steel ball (sphere, s=8.0) to conduct the test. From the tests, she found that the terminal velocity of the sphere was 2.5 fpm. What is the viscosity of the oil? Remember, the volume of a sphere is (pi D3 /6). ANS. viscosity is 0.258 lb-s/ft2

Answer 1

0.25916 lb-s/ft^2

Step-by-step explanation:

Given:-

- The specific gravity of oil, SGo = 0.8

- The specific gravity of sphere, SGo = 8

- Terminal velocity of sphere, v = 2.5 fpm

- The diameter of sphere, D = 0.25 in

Find:-

What is the viscosity of the oil?

Solution:-

- Consider a sphere completely submerged into oil and travelling with terminal velocity ( v ).

- Develop a free body diagram for the sphere. There are forces acting on the sphere.

- The downward acting force is due to the weight of the sphere ( W ):

`W = m_s*g`

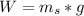
Where,

The mass ( m_s ) of the sphere is given as:

`m_s = S.G_s*p_w*V_s`

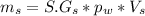
Where,

ρ_w : Density of water = 1.940 slugs/ft3

V_s: The volume of object ( sphere )

- The volume of sphere is expressed as a function of radius:

`V_s = (\pi *D^3)/(6)`

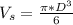
Hence,

`W = S.G_s*p_w*(\pi*D^3 )/(6)* g\\\\W = 8*1.940*(\pi*(0.25/12)^3 )/(6)*32\\\\W = 0.00235 lb`

- One of the upward acting force is the buoyant force ( Fb ) that is proportional to the volume of fluid displaced by the immersed object.

- The buoyant force ( Fb ) is given by:

`F_b = S.G_o*p_w*V_s*g`

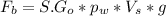
- Therefore the buoyant force ( Fb ) becomes:

`F_b = 0.8*1.94*(\pi*(0.25/12)^3 )/(6) *32\\\\F_b = (4.73451*10^-^6)*(49.664)\\\\F_b = 0.00023 lb`

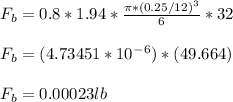
- The other upward acting force is the frictional drag ( F_d ) i.e the resistive frictional force acting on the contact points of the sphere and the fluid oil.

- From stokes formulations the drag force acting on a spherical object which is completely immersed in a fluid is given as:

`F_d = 3*\pi*D*u*v`

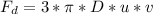
Where,

μ: The viscosity of fluid

v : The velocity of object

Therefore,

`F_d = 3*\pi*(0.25)/(12) *u*0.041666\\\\F_d = 0.00818*u\\`

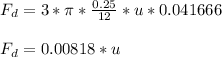
- Apply Newton's second law of motion for the sphere travelling in the fluid:

`F_n_e_t = m_s*a`

Where,

a: Acceleration of object = 0 ( Terminal velocity condition )

`F_n_e_t = 0`

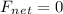
- Plug in the three forces acting on the metal sphere:

`F_d + F_b - W = 0\\\\F_d = W - F_b\\\\0.00818*u = 0.00235 - 0.00023\\\\u = (0.00212)/(0.00818) = 0.25916 (lb-s)/(ft^2)`