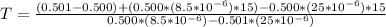Answer:
The temperature is

Step-by-step explanation:
From the question we are told that
The temperature is
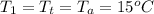
The diameter is
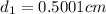
The diameter of the hole
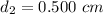
The coefficient of linear expansion for aluminum is
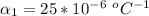
The coefficient of linear expansion for titanium is

According to the law of linear expansion

Where
 represents the original diameter
represents the original diameter
So for aluminum
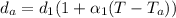
Where
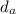 is the new diameter of aluminum
is the new diameter of aluminum
 is the new temperature of the aluminum
is the new temperature of the aluminum
So for titanium
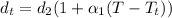
Where
 is the new diameter of titanium
is the new diameter of titanium
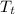 is the new temperature of the aluminum
is the new temperature of the aluminum
So for the aluminum rivets to fit into the holes

=>
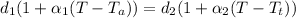
Making T the subject of the formula
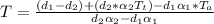
Substituting values