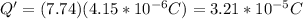Question

15. A parallel-plate capacitor, with air between the plates, is connected across a voltage source. This source establishes a potential difference between the plates by placing charge of magnitude 4.15 x 10-6 C on each plate. The space between the plates is then filled with a dielectric material, with a dielectric constant of 7.74. What must the magnitude of the charge on each capacitor plate now be, to produce the same potential difference between the plates as before? (Input your answer in 3 significant figures without unit. For example, if the answer is 1.356 x 10-6 C; then just input 1.37)

Answer 1

Q' = 3.21*10^{-5}C

Step-by-step explanation:

To find the new magnitude of the charge you take into account that the voltage of the this capacitor is given by:

`(Q)/(\epsilon_o\epsilon_r A)=(V)/(d)\\\\V=(Qd)/(\epsilon_o\epsilon_r A)`

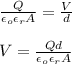
Q: total charge

d: distance between parallel plates

A: area of the plates

εr: dielectric constant

εo = dielectric permittivity of vacuum

for the case of the air εr = 1, then,

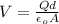`V=(Qd)/(\epsilon_o A)` (1)

When a dielectric material is placed in between the plates, you have, for the same voltage, and for a different charge:

`V=(Q'd)/(\epsilon_o\epsilon_rA)` (2)

you equal the equation (1) and (2) and obtain:

`(Qd)/(\epsilon_o A)=(Q'd)/(\epsilon_o \epsilon_r A)\\\\Q'=\epsilon_r Q`

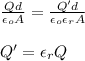
by replacing you obtain:

`Q'=(7.74)(4.15*10^(-6)C)=3.21*10^(-5)C`