Answer:
(a) Probability that a family of a returning college student spend less than $150 on back-to-college electronics is 0.0537.
(b) Probability that a family of a returning college student spend more than $390 on back-to-college electronics is 0.0023.
(c) Probability that a family of a returning college student spend between $120 and $175 on back-to-college electronics is 0.1101.
Explanation:
We are given that according to an NRF survey conducted by BIG research, the average family spends about $237 on electronics in back-to-college spending per student.
Suppose back-to-college family spending on electronics is normally distributed with a standard deviation of $54.
Let X = back-to-college family spending on electronics
SO, X ~ Normal(
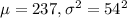 )
)
The z score probability distribution for normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean family spending = $237
= population mean family spending = $237
 = standard deviation = $54
= standard deviation = $54
(a) Probability that a family of a returning college student spend less than $150 on back-to-college electronics is = P(X < $150)
P(X < $150) = P(
 <
<
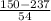 ) = P(Z < -1.61) = 1 - P(Z
) = P(Z < -1.61) = 1 - P(Z
 1.61)
1.61)
= 1 - 0.9463 = 0.0537
The above probability is calculated by looking at the value of x = 1.61 in the z table which has an area of 0.9463.
(b) Probability that a family of a returning college student spend more than $390 on back-to-college electronics is = P(X > $390)
P(X > $390) = P(
 >
>
 ) = P(Z > 2.83) = 1 - P(Z
) = P(Z > 2.83) = 1 - P(Z
 2.83)
2.83)
= 1 - 0.9977 = 0.0023
The above probability is calculated by looking at the value of x = 2.83 in the z table which has an area of 0.9977.
(c) Probability that a family of a returning college student spend between $120 and $175 on back-to-college electronics is given by = P($120 < X < $175)
P($120 < X < $175) = P(X < $175) - P(X
 $120)
$120)
P(X < $175) = P(
 <
<
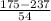 ) = P(Z < -1.15) = 1 - P(Z
) = P(Z < -1.15) = 1 - P(Z
 1.15)
1.15)
= 1 - 0.8749 = 0.1251
P(X < $120) = P(
 <
<
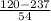 ) = P(Z < -2.17) = 1 - P(Z
) = P(Z < -2.17) = 1 - P(Z
 2.17)
2.17)
= 1 - 0.9850 = 0.015
The above probability is calculated by looking at the value of x = 1.15 and x = 2.17 in the z table which has an area of 0.8749 and 0.9850 respectively.
Therefore, P($120 < X < $175) = 0.1251 - 0.015 = 0.1101