Question

11. Two radio antennas are 120 m apart on a north-south line, and they radiate in phase at a frequency of 3.4 MHz. All radio measurements are made far from the antennas. If the east-west reference line passes midway between the two antennas, what is the smallest angle in degree from the antennas, measured north of east, at which constructive interference of two radio waves occurs? (c = 3.00 × 108 m/s) (Input your answer in 2 significant figures without unit)

Answer 1

47°

Step-by-step explanation:

between the two antennas for an observer difference in length in quadrant I is

ΔL = dCos(θ)

setting θ=0 i.e the observer is north of the station to get

ΔL= d= 120 m.

The wavelength formula is:

λ = c / f = 3x
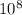`10^8` / 3.4 x
`10^6` = 88.2m

Constructive interference occurs when the Length difference is equal to an integer multiple of a wavelength.

At the given spacing, and from an observation point north of the stations, they are more than a wavelength apart, so they are not in constructive interference. Looking for the first peak:

dCos(θ) = λ

Cos(θ) = λ/d

θ = arcCos(λ/d) = arcCos( 88.2 / 120 ) = 42.7°= 43°

For destructive interference:

90° - 43°= 47°