Question

An electric dipole consists of a positive and a negative charge of equal magnitude. Consider an electric dipole with each charge having a magnitude of 1 × 10−6 C. The negative charge is located at (3 cm, 0) and the positive charge is located at (−3 cm, 0). Calculate the electric field from each charge at the points A through E, described below. Use symmetry as much as possible! Using the scale 1 cm = 105 N/C, draw the vector to represent the magnitude and direction of the electric field from each charge. (When entering angle values, enter a number greater than or equal to 0° and less than 360° measured counterclockwise from the +x-axis.) • A = (−13 cm, 0) • B = (−3 cm, 10 cm) • C = (0, 10 cm ) • D = (3 cm, 10 cm) • E = (13 cm, 0) For the negative charge:

Answer 1

Step-by-step explanation:

To find the electric field you use the equation for an electrostatic electric field:

`E=k(q_1q_2)/(r^2)`

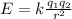
r: distance in which E is calculated, from each charge

In the of a dipole you have two contributions to E:

`\vec{E}=\vec{E_1}+\vec{E_2}`

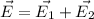
where E1 is the electric field generated by the first charge and E2 by the second one.

A. (-13 cm, 0):

First you calculate the vectors E1 and E2:

`E_1=(8.98*10^9)((1*10^(-6)C))/((-0.13-0.03)^2)\hat{j}\\\\E_1=350781.25N/C\\\\E_2=-(8.98*10^9)((1*10^(-6)C))/((-0.13+0.03)^2)\hat{j}\\\\E_2=-989000N/C`

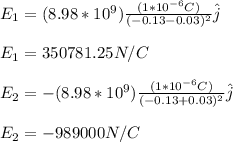
Then, you sum both contributions:

`\vec{E}=-547218.75N/C\hat{j}`

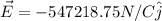
B. (-3cm, 10cm):

`r_1=√((0.06)^2+(0.1)^2)=0.116m\\\\\theta=tan^(-1)((0.06)/(0.1))=30.96\°\\\\r_2=0.1m\\\\E_1=(8.98*10^9Nm^2/C)((1.6*10^(-6)C))/((0.116m)^2)[cos(30.96\°)\hat{i}+sin(30.96\°)\hat{j}]\\\\E_1=[-915646\hat{i}-549306.42\hat{j}]N/C\\\\\theta=(90-30.96)+180=239.04\°\\\\`

the last angle is calculated again because the vector direction is measured from the +x axis.

and for the second vector:

`E_2=(8.98Nm^2/C)(1.6*10^(-6)C)/((0.1m)^2)\hat{j}\\\\E_2=1436800N/C\hat{j}`

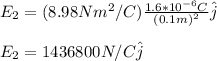
the total E is:

`\vec{E}=[-915646\hat{i}+887493.58\hat{j}]N/C`