Question

The uniform slender bar of mass m and length l is released from rest in the vertical position and pivots on its square end about the corner at O. (a) If the bar is observed to slip when   30 , find the coefficient of static friction s between the bar and the corner. (b)If the end of the bar is notched so that it cannot slip, find the angle  at which contact between the bar and the corner ceases.

Answer 1

A) 0.188

B) 53.1 ⁰

Step-by-step explanation:

taking moment about 0

∑ Mo = Lo∝

mg 1/2 sin∅ = 1/3 m L^2∝

note ∝ = w
`(dw)/(d)`∅

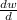forces acting along t-direction ( ASSUMED t direction)

∑ Ft = Ma(t) = mr∝

mg sin ∅ - F = m* 1/2 * 3g/2l sin∅

therefore F = mg/4 sin∅

forces acting along n - direction ( ASSUMED n direction)

∑ Fn = ma(n) = mr(
`w^(2)`)

= mg cos∅ - N = m*1/2*3g/1 ( 1 - cos∅ )

hence N = mg/2 ( 5cos∅ -3 )

A ) Angle given = 30⁰c find coefficient of static friction

∪ = F/N

=
`((mg)/(4)sin30 )/((mg)/(2)(5cos30 -3) )` = 0.188

B) when there is no slip

N = O

= 5 cos ∅ -3 =0

therefore cos ∅ = 3/5 hence ∅ = 53.1⁰