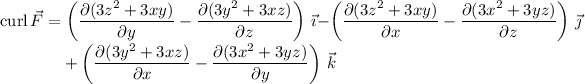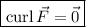Since F is apparently a vector field, I assume you mean
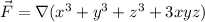
with ∇ = gradient, whereas ∆ is often used to denote the Laplacian, ∆ = ∂²/∂x² + ∂²/∂y² + ∂²/∂z².
Let
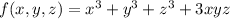 . Compute the gradient of f :
. Compute the gradient of f :
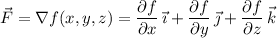
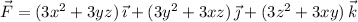
Now compute the divergence of F (incidentally, divergence of a gradient field is the Laplacian of the f):
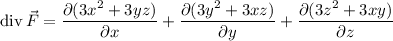
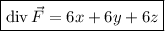
and the curl: (the following is overkill, since any gradient field has curl zero, but it doesn't hurt to verify that)