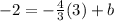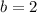Answer:
Question A, the values of h is 11 and k is -8 .
Question B, the equation is y = (-4/3)x + 2 .
Explanation:
Question A, in order to find the value of h and k, you have to use the mid-point formula and do comparison :
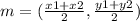
Let (x1,y1) be coordinate A (h,4),
Let (x2,y2) be coordinate B (-5,k),
Let mid-point be (3,-2),
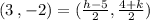
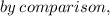
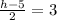
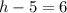
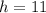
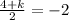
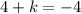
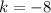
Question B, given that line is perpendicular bisetor to AB means that the line touches mid-point which is M(3,-2). Using gradient formula :
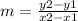
Let (x1,y1) be (11,4),
Let (x2,y2) be (-5,-8),
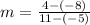
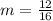
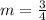
The gradient of perpendicular line is opposite of line AB and when both gradient are multiplied, you should get -1 :
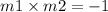
Let m1 be the gradient of AB, m = 3/4,
Let m2 be the gradient of perpendicular line,
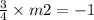
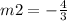
Last, we have to use the slope-form equation, y = mx + b and susbtitute the coordinates of M into the equation :
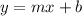
Let m = -4/3,
Let x = 3,
Let y = -2,