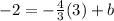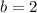Question

6 The midpoint of the line segment joining

Alh, 4) and B(-5, k) is M(3,-2). Find
(a) the values of h and k,
(b) the equation of the perpendicular
bisector of the line segment AB.​

Answer 1

Question A, the values of h is 11 and k is -8 .

Question B, the equation is y = (-4/3)x + 2 .

Explanation:

Question A, in order to find the value of h and k, you have to use the mid-point formula and do comparison :

`m = ( (x1 + x2)/(2) , (y1 + y2)/(2) )`

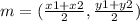
Let (x1,y1) be coordinate A (h,4),

Let (x2,y2) be coordinate B (-5,k),

Let mid-point be (3,-2),

`(3 \: , - 2) = ( (h - 5)/(2) , (4 + k)/(2) )`

`by \: comparison, \:`

`(h - 5)/(2) = 3`

`h - 5 = 6`

`h = 11`

`(4 + k)/(2) = - 2`

`4 + k = - 4`

`k = - 8`

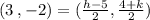
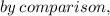
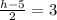
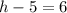
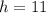
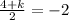
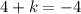
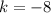
Question B, given that line is perpendicular bisetor to AB means that the line touches mid-point which is M(3,-2). Using gradient formula :

`m = (y2 - y1)/(x2 - x1)`

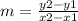
Let (x1,y1) be (11,4),

Let (x2,y2) be (-5,-8),

`m = (4 - ( - 8))/(11 - ( - 5))`

`m = (12)/(16)`

`m = (3)/(4)`

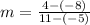
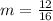
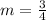
The gradient of perpendicular line is opposite of line AB and when both gradient are multiplied, you should get -1 :

`m1 * m2 = - 1`

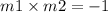
Let m1 be the gradient of AB, m = 3/4,

Let m2 be the gradient of perpendicular line,

`(3)/(4) * m2 = - 1`

`m2 = - ( 4)/(3)`

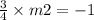
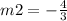
Last, we have to use the slope-form equation, y = mx + b and susbtitute the coordinates of M into the equation :

`y = mx + b`

Let m = -4/3,

Let x = 3,

Let y = -2,

`- 2 = - (4)/(3) (3) + b`

`b = 2`