Answer:
44 square units
Explanation:
The area of a trapezoid with bases b₁ and b₂ and height h is given by the formula
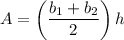
If you're wondering how we get this formula, check the attached illustration (remember the area of a parallelogram is its base multiplied by its height)! Moving on to our trapezoid, the pairs of points (-5,-3)(4,-3) and (6,-7)(-7,-7) form two horizontal segments, which form b₁ and b₂, and our height is the distance between the y-coordinates -3 and -7, which is 4. We can find b₁ and b₂ by finding the distance between the x coordinates in their pairs of points:

Putting it altogether:
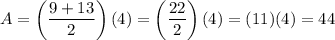
So the area of our trapezoid is 44.