Answer:
A and B.
Explanation:
If we simplified this equation, we could begin by dealing with the exponents inside of the parenthesis. Remember, when multiplying you will need to add exponents.
This gives us:
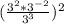 -->
-->
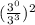
Simplifying this gets us:

Now, multiply the exponent outside of the parenthesis with the exponent inside resulting in:
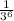
----------------------------------
Reasoning for answer A:
The step of multiplying the outside exponents with those inside was done first:
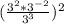 -->
-->
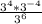
Therefore, we get answers A and B.