We have been given a circle H, in which length of arc XY is 78 miles and measure of arc XY is 70 degrees. We are asked to find the radius of circle.
We will use arc length formula to solve our given problem.
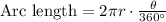 , where,
, where,
r = Radius of circle,
 = Central angle corresponding to arc.
= Central angle corresponding to arc.
We know that the measure of central angle that corresponds to arc XY will be equal to measure of arc XY.
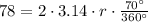
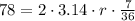
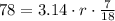
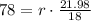
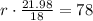
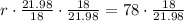
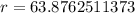
Upon rounding to nearest hundredth, we will get:
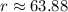
Therefore, the radius of circle H is approximately 63.88 miles.