Question

The graph of F(x), shown below in pink, has the same shape as the graph of

G(X) = x2, but it is flipped over the x-axis and shifted down 1 unit. What is its
equation?

Answer 1

We have been given that the graph of
`F(x)` has the same shape as the graph of
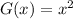`G(x)=x^2`, but it is flipped over the x-axis and shifted down 1 unit. We are asked to find the equation of
`F(x)`.

We will use transformation rules to solve our given problem.

The rule of reflection of a graph about x-axis is
`f(x)\Rightarrow -f(x)`.

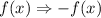Let us find
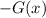`-G(x)` as:

`-G(x)=-(x^2)=-x^2`

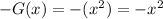
Now we will shift our graph 1 unit down.

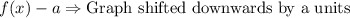`f(x)-a\Rightarrow\text{Graph shifted downwards by a units}`, where a is a positive number.

This is same as subtracting 1 from
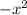`-x^2` as:

`F(x)=-x^2-1`

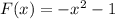
Therefore, our required function would be
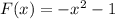`F(x)=-x^2-1`.