Question

HELPPPP

Scores on a math placement exam at UGA are normally distributed with a mean of 76 and a standard deviation of 6. What is the probability that an incoming freshman scores between 61.6 and 80.2?

Answer 1

The probability that an incoming freshman scores between 61.6 and 80.2 is 0.7498

Explanation:

We are given that Scores on a math placement exam at UGA are normally distributed with a mean of 76 and a standard deviation of 6.

Mean =
`\mu = 76`

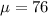
Standard deviation =
`\sigma = 6`

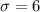
we are supposed to find the probability that an incoming freshman scores between 61.6 and 80.2 i.e. P(61.6<x<80.2)

Formula :
`Z=(x-\mu)/(\sigma)`

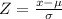
At x = 61.6

So,
`Z=(61.6-76)/(6)`

Z=-2.4

Refer the z table for p value

So,p value =0.0082

At x = 80.2

So,
`Z=(80.2-76)/(6)`

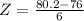
Z=0.7

Refer the z table for p value

So,p value =0.7580

P(61.6<x<80.2)=P(x<80.2)-P(x<61.6)=0.7580-0.0082=0.7498

Hence the probability that an incoming freshman scores between 61.6 and 80.2 is 0.7498