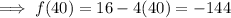Answer:
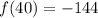
Explanation:
Given:
This is a recursive arithmetic sequence since each term is defined using the previous term.
To find the nth term, convert the recursive formula to an explicit formula.
Explicit form of an arithmetic sequence:
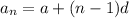
where:
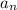 is the nth term
is the nth term- a is the first term
- d is the common difference between terms
We have been given the first term:
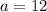
To get any term from its previous term we subtract 4, so the common different (d) is -4.
Therefore, the formula for the nth term is:
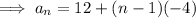
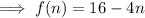
To find
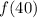 simply substitute n = 40 into the explicit formula:
simply substitute n = 40 into the explicit formula: