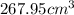Answer:
Explanation:
We need to first find the radius of the sphere.
The surface area of a sphere is given as:
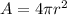
where r is the radius
Therefore:
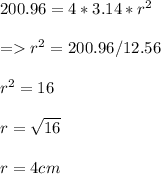
The radius of the sphere is 4 cm.
The volume of a sphere is given as:
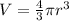
Therefore, the volume of the sphere of radius 4 cm is;
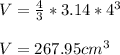
The volume of the sphere is