Answer: 226 grams
===========================================================
Step-by-step explanation:
The half-life is 35 hours. This means every 35 hours, the amount of the substance is cut in half. If we started with 100 grams, then 35 hours later, we will have 50 grams. Then another 35 hours later we will then have 25 grams, and so on.
In this case, we start with 904 grams and follow this sequence:
904, 452, 226, 113, ...
Each term is cut in half. Going from term to term it takes 35 hours each. The third term 226 is the result of waiting two half-lives, which is 2*35 = 70 hours that have elapsed total.
--------------
If you want to use a formula, then it would be
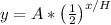
where,
H = half-life duration (in this case, it is 35)
A = starting amount (which is 904 in this case)
x = amount of time that has elapsed (we will plug in x = 70)
y = final amount after x units of time has elapsed
note that x and H must have the same time unit. Both are in terms of hours in this case.
------------
So we will plug A = 904, x = 70, H = 35 into the formula to get...
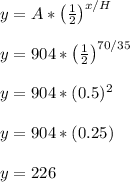
We see that x = 70 leads to y = 226. This means after 70 hours, there is 226 grams of the material left.