Answer:

Explanation:
Let A be the event of getting an odd number.
P(A) be the probability of getting an odd number.
Total odd numbers here are 6 i.e.

Here, total numbers in the game are 12 i.e
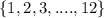 .
.
Formula for probability of an event E can be observed as:
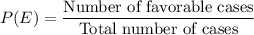
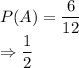
Let B be the event of getting 11.
P(B) be the probability of getting 11.
Total number of possible cases is 1.
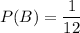
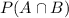 is the probability that we get 11 and an odd number.
is the probability that we get 11 and an odd number.
Possible number of cases = 1
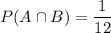
P(B/A) is the probability that we get an 11 given that it is an odd number.
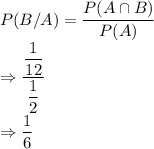
Hence, P(B/A) =
