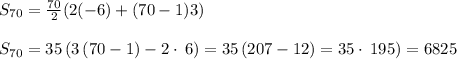Question

Find the sum of the first 70 terms of the sequence -6, -3,0,3,6,​

Answer 1

The sum of the first 70 terms of the sequence
`-6, -3,0,3,6, ...` is 6825.

Explanation:

A sequence is a set of numbers that are in order.

In an Arithmetic Sequence the difference between one term and the next is a constant.

`-6, -3,0,3,6, ...` This sequence has a difference of 3 between each number.

The sum of an arithmetic series is found by multiplying the number of terms times the average of the first and last terms.

`S_n=(n)/(2)(2a_1+(n-1)d)`

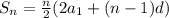
where
`n` = the number of terms,
`a_1` = the first term, and
`d` = the common difference.

For our arithmetic sequence, the values of a, d and n are:

• 
  `a_1 =-6`
• 
  `d=3`
• 
  `n = 70`

So:

`S_(70)=(70)/(2)(2(-6)+(70-1)3)\\\\S_(70)=35\left(3\left(70-1\right)-2\cdot \:6\right)=35\left(207-12\right)=35\cdot \:195)=6825`