Answer:
Probability that 3 out of the next 5 voters approving the proposal is 0.3125.
Explanation:
We are given that the sample probability of the voters approving the proposal is 50% and Political scientists want to determine the probability of exactly 3 out of the next 5 voters they meet approving a proposal.
The above situation can be represented through binomial distribution;
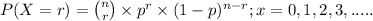
where, n = number of trials (samples) taken = 5
r = number of success = exactly 3
p = probability of success which in our question is probability of
the voters approving the proposal, i.e; p = 50%
Let X = Number of voters approving the proposal
So, X ~ Binom(n = 5 , p = 0.50)
Now, Probability that 3 out of the next 5 voters approving the proposal is given by = P(X = 3)
P(X = 3) =
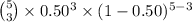
=

= 0.3125