Answer:
3
Explanation:
Given:
Team heights (inches):
61, 57, 63, 62, 60, 64, 60, 62, 63
To find: IQRs (interquartile ranges) of the heights for the team
Solution:
A quartile divides the number of terms in the data into four more or less equal parts that is quarters.
For a set of data, a number for which 25% of the data is less than that number is known as the first quartile

For a set of data, a number for which 75% of the data is less than that number is known as the third quartile
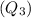
Terms in arranged in ascending order:
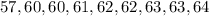
Number of terms = 9
As number of terms is odd, exclude the middle term that is 62.
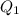 is median of terms
is median of terms
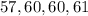
Number of terms (n) = 4
Median =

So,
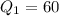
So, 25% of the heights of a team is less than 60 inches
 is the median of terms
is the median of terms
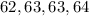
Median =
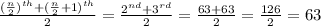
So,
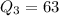
So, 75% of the heights of a team is less than 63 inches
Interquartile range =
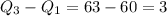
The interquartile range is a measure of variability on dividing a data set into quartiles.
The interquartile range is the range of the middle 50% of the terms in the data.
So, 3 is the range of the middle 50% of the heights of the students.