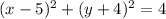Answer:
The equation of a circle is
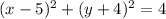 .
.
Explanation:
-The equation of a circle is:
 (where center is
(where center is
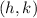 , the point
, the point
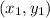 and the radius known as
and the radius known as
 ).
).
-Use the center (5,-4) and the point (5,-2) for the equation:
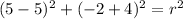
-Solve the equation:
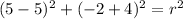

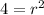
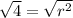
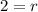
-After you found the radius, use the center (5, -4) and radius 2 to get the equation of a circle:
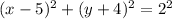
-Then, after you have the equation, the radius needs to simplified by the exponent: