Question

What is the value of x in the equation.

2/3(1/2x+12)=1/2(1/3x+14)-3?
A:-24
B:-6
C:-2/3
D:0

Answer 1

A

Explanation:

Our equation is:

`(2)/(3) *((1)/(2) x+12)=(1)/(2) *((1)/(3) x+14)-3`

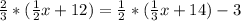
Let's first distribute the left side. When distributing, we essentially find the sum of the product of the outside term with each of the inside terms. Here, the outside term is 2/3 and the inside terms are 1/2x and 12. So:

`(2)/(3) *((1)/(2) x+12)=(2)/(3) *(1)/(2) x+(2)/(3) *12=(1)/(3) x+8`

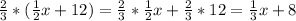
Now distribute the right side. Here, the outside term is 1/2 and the inside terms are 1/3x and 14, so:

`(1)/(2) *((1)/(3) x+14)-3`

`(1)/(2) *((1)/(3) x+14)-3=(1)/(2) *(1)/(3) x+(1)/(2) *14-3=(1)/(6) x+7-3=(1)/(6) x+4`

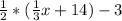
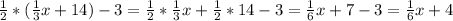
We now have:

`(1)/(3) x+8=(1)/(6) x+4`

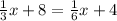
Isolate the variable by bringing 1/6x to the left and bringing 8 to the right:

`(1)/(3) x-(1)/(6) x=4-8`

`(2)/(6) x-(1)/(6) x=-4`

`(1)/(6) x=-4`

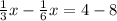
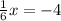
x = -4 * 6 = -24

The answer is A.

Answer 2

Steps to solve:

2/3(1/2x + 12) = 1/2(1/3x + 14) - 3

~Distribute

1/3x + 8 = 1/6x + 7 - 3

~Combine like terms

1/3x + 8 = 1/6x + 4

~Subtract 1/6x to both sides

1/3x + 8 - 1/6x = 1/6x + 4 - 1/6x

~Simplify

1/6x + 8 = 4

~Subtract 8 to both sides

1/6x + 8 - 8 = 4 - 8

~Simplify

1/6x = -4

~Multiply 6 to both sides

1/6x * 6 = -4 * 6

~Simplify

x = -24

Best of Luck!