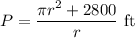Question

Problem 5. A skating rink in the shape shown has an area of

2,800 ft”. Find a formula for the perimeter of the rink as a
function of the radius r.

Answer 1

`P=(\pi r^2+2800)/(r) $ ft`

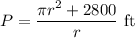
Explanation:

Let the length of the rectangular part =l

The width will be equal to the diameter of the semicircles.

Area of the Skating Rink=
`2((\pi r^2)/(2))+(lX2r)`

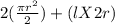
Therefore:

`\pi r^2+2lr=2800\\2lr=2800-\pi r^2\\$Divide both sides by 2r\\l=(2800-\pi r^2)/(2r)`

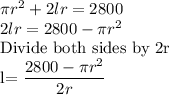
Perimeter of the Shape =Perimeter of two Semicircles + 2l

`=2\pi r+2\left((2800-\pi r^2)/(2r)\right)\\=2\pi r+(2800-\pi r^2)/(r)\\=(2\pi r^2+2800-\pi r^2)/(r)\\=(\pi r^2+2800)/(r)`

The perimeter of the rink is given as:

`P=(\pi r^2+2800)/(r) $ ft`