Answer:
A. volume of the metal used to build the pipe is 141
 cubic inches.
cubic inches.
B. The total surface area to be powder coated is 1122.125 square inches.
Explanation:
The length of the cylinder = 4 feet = 48 inches.
Radius of the outside of the pipe = 6 inches.
Radius of the inside of the pipe = 5.75 inches
A. volume of the metal used to build the pipe = volume of the outside pipe - volume of the inside pipe
volume of a cylinder =

 h
h
volume of the outside pipe =

 h
h
=
 ×
×
 × 48
× 48
= 1728
 cubic inches
cubic inches
volume of the inside pipe =

 h
h
=
 ×
×
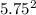 × 48
× 48
= 1587
 cubic inches
cubic inches
volume of the metal used to build the pipe = 1728
 - 1587
- 1587

= 141
 cubic inches
cubic inches
B. Total surface area of a hollow cylinder = 2
 (
(
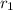 +
+
 ) (
) (
 -
-
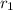 + h)
+ h)
where
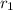 is the inner radius and
is the inner radius and
 is the outer radius.
is the outer radius.
= 2
 (6 + 5.75)(5.75 - 6 + 48)
(6 + 5.75)(5.75 - 6 + 48)
= 2
 (11.75 × 47.75)
(11.75 × 47.75)
= 1122.125
 square inches
square inches
The total surface area to be powder coated is 1122.125 square inches.