Question

A college statistics class at a nearby university has 1,000 students enrolled in it. On a recent exam, the mean score was 75% with a standard deviation of 5%. Use the calculator to show what percentage of students scored between a 73 and 78 (C grade).

Answer 1

38.11%

Explanation:

Given that:

Mean (μ) = 75, standard deviation (σ) = 5

Z score is a measure in statistics to determine the variation of a raw score from the mean. It is given by the equation:

`z=(x-\mu)/(\sigma)`

To calculate the percentage of students scored between a 73 and 78 (C grade), we need to find the z score for 73 and then for 78.

For x = 73, the z score is:

`z=(x-\mu)/(\sigma)=(73-75)/(5) =-0.4`

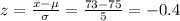
For x = 78, the z score is:

`z=(x-\mu)/(\sigma)=(78-75)/(5) =0.6`

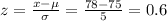
From the probability distribution table:

P(73 < x < 78) = P(-0.4 < z < 0.6) = P(z < 0.6) - P(z < -0.4) = 0.7257 - 0.3446 = 0.3811 = 38.11%