Answer:
Total amount to be paid on 13th day is $40.96.
Explanation:
Mr. Morris pays Rob $0.01, $0.02, $0.04 ..... on 1st, 2nd , 3rd .... day respectively.
We can clearly see that the next number is becoming double of the previous value.
The above sequence of numbers are in a Geometric Progression with
First term, a = 0.01 and
Common ratio, r = 2
We have to find the total amount paid on 13th day.
We know that the
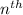 term of a GP is given by:
term of a GP is given by:
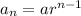
Where, a is the first term of GP
r is the common ratio
We have to find the
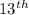 term of the GP as per question statement.
term of the GP as per question statement.
Putting the values in the formula above:
n = 13
a = 0.01 and
r = 2
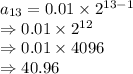
Total amount to be paid on 13th day is $40.96.