Answer:
The attendance was 198 children, 90 students and 99 adults.
Explanation:
We define:
c: children attendance
s: students attendance
a: adult attendance
The equation that describes the total ticket sales is:
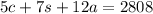
We also know that the children attendance doubles the adult attendance:
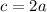
The third equation is the seating capacity, which we assume is full:
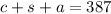
We start by replacing variables in two of the equations:

Then, we solve the remaining equation for a:
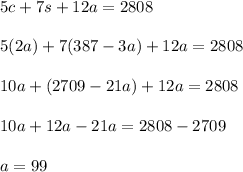
Then, we solve for the other two equations:
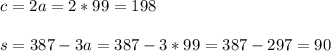
The attendance was 198 children, 90 students and 99 adults.