Answer:
5. m∠C ≈ 34°
6. AC ≈ 29.7 metres
Explanation:
5. We need to use the Law of Sines here, which says that for a triangle with sides a, b, and c and angles A, B, and C:
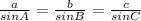
Here, a = 25, ∠A = 93°, and c = 14, so we want to find ∠C:
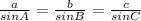

sinC ≈ 0.56
∠C ≈ 34°
6. We need to use the Law of Cosines here, which says that for a triangle with sides a, b, and c and angles A, B, and C:
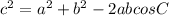


Here, a = 23.2, c = 18.1, ∠B = 91°, and b = x. We want to find b, so:

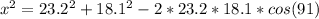 ≈ 880.5
≈ 880.5
x ≈ 29.7 metres