Question

A 0.009 kg bullet fired through a door enters at 803 m/s and leaves at 617 m/s. If the door material is known to exert an average resistive force of 5620 N on bullets of this type at usual speeds, find the thickness of the door.

Answer 1

The thickness of the door is 0.4230 m

Step-by-step explanation:

Given;

mass of bullet, m = 0.009 kg

initial velocity of the bullet, u = 803 m/s

final velocity of the bullet, v = 617 m/s

average resistive force of the door on the bullet, F = 5620 N

Apply Newton's second law of motion;

Force exerted by the door on the bullet = Force of the moving bullet

F = ma

where;

F is applied force

m is mass

a is acceleration

Also, Force exerted by the door on the bullet = Force of the moving bullet

`F =ma, \ But \ a =(dv)/(dt) = (u-v)/(t) \\\\F = (m(u-v))/(t)`

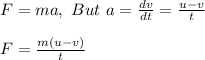
where;

v is the final velocity of the bullet

u is initial velocity of the bullet

t is time

We need to calculate the time spent by the bullet before it passes through the door.

`t = (m(u-v))/(F) \\\\t = (0.009(803-617))/(5620) = 0.0002979 \ s`

Distance traveled by the bullet within this time period = thickness of the door

This distance is equivalent to the product of average velocity and time

`S = ((u+v)/(2)) t`

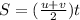
where;

s is the distance traveled

`S = ((u+v)/(2)) t\\\\S = ((803+617)/(2)) 0.0002979\\\\S = 0.4230 \ m`

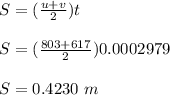
Therefore, the thickness of the door is 0.4230 m