Answer:
200 minutes
Explanation:
To find this, you should first set up an equation. Since you are trying to find the point where both plans cost the same, set them equal to each other. Let x be the cost for both. Write the equation:
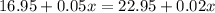
We place the x with the cost per minute because this is what you are trying to find. We add the cost per month.
Solve for x. Subtract 16.95 from both sides and simplify:
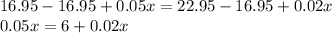
Subtract 0.02x from both sides:
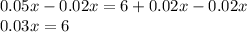
Divide both sides by 0.03:
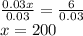
At 200 minutes, the cost for both plans would be the same.