Question

You have a jar of marbles with 7 red, 12 blue, 6 yellow, and 9 white. What is the probability of selecting a marble that is not red, replacing it and then one that

is white?​

Answer 1

The probability of selecting a marble that is not red, replacing it and then one that is white is 0.2102

Explanation:

Number of red marbles = 7

Number of blue marbles = 12

Number of yellow marbles = 6

Number of white marbles = 9

Total marbles = 7+12+6+9=34

Probability of selecting red marble =
`(7)/(34)`

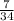
Probability of selecting no red marble =
`1-(7)/(34)=(27)/(34)`

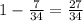
Now replacing it one marble is drawn again

So, Probability of getting white marble
`=(9)/(34)`

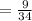
So,the probability of selecting a marble that is not red, replacing it and then one that is white =
`(27)/(34) * (9)/(34)=0.2102`

Hence the probability of selecting a marble that is not red, replacing it and then one that is white is 0.2102