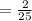Question

In a certain Algebra 2 class of 25 students, 5 of them play basketball and 10 of them play baseball. There are 12 students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball?

Answer 1

Probability of students who plays both baseball and basketball is
`(2)/(25)`

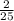
Explanation:

We have given total number of students = 25

5 of them play basket ball 10 of them plays base ball

there are 12 students who neither play baseball nor basket ball

So the number of students who play either baseball or basketball is

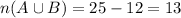`n(A\cup B)=25-12=13`, here A is for basketball and B is for baseball.

From set theory we know that

`n(A\cup B)=n(A)+n(B)-n(A\cap B)`

`13=5+10-n(A\cap B)`

`n(A\cap B)=2`

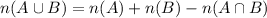
Therefore there are two students who play both baseball and basketball

Probability is equal to
`=(2)/(25)`