Answer:
1) True, True, False
Rewritten statement: 46,013.86 cm³ of water was used to fill 40 balloons
2) False, True, True
Rewritten statement: The formula
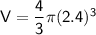 can be used to find the volume of the model of Earth.
can be used to find the volume of the model of Earth.
3) True, False, True
Rewritten statement: The volume of all the basketballs is 13,467.62 in³
Explanation:
Question 1
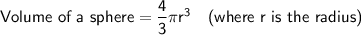
Given:
Substituting the given radius into the formula:
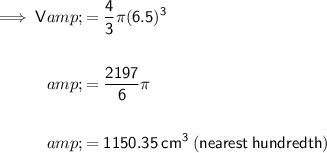
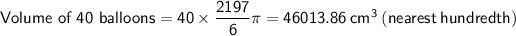
Rewritten statement: 46,013.86 cm³ of water was used to fill 40 balloons
-------------------------------------------------------------------------------------------------------
Question 2
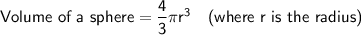
Earth
Given:
- diameter = 4.8 cm ⇒ r = 2.4 cm
Substituting the given radius into the formula:
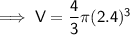

Rewritten statement:
The formula
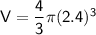 can be used to find the volume of the model of Earth.
can be used to find the volume of the model of Earth.
Saturn
Given:
- diameter = 45.6 cm ⇒ r = 22.8 cm
Substituting the given radius into the formula:
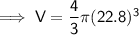
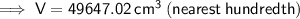
Difference between models= 49,647.02 - 57.91 = 49,589.11 cm³
-------------------------------------------------------------------------------------------------------
Question 3
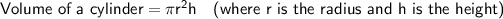
Given:
Substituting the given values into the formula:


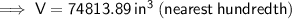
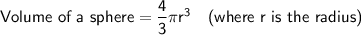
Given:
- diameter = 9.5 in ⇒ r = 4.75 in
- 30 basketballs
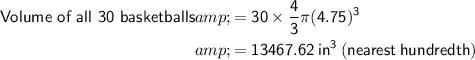
Rewritten statement: The volume of all the basketballs is 13,467.62 in³
Empty space in the container = volume of container - volume of basketballs
⇒ 74813.89 - 13467.62 = 61,346.27 in³