Question

A population is growing continuously at a rate of 5%. If the population is now 3400, what will it be in 17 years? Round to the nearest thousand.

Answer 1

Explanation:

The growth rate is exponential. We would apply the formula for exponential growth which is expressed as

y = b(1 + r)^ t

Where

y represents the population after t years.

t represents the number of years.

b represents the initial population.

r represents rate of growth.

From the information given,

b = 3400

r = 5% = 5/100 = 0.05

t = 17 years

Therefore

y = 3400(1 + 0.05)^17

y = 3400(1.05)^17

y = 3400 × 2.2920183178

y = 7800 to the nearest thousand

Answer 2

In 17 years time, the initial population of 3400, and growing at a rate of 5% will be ≈ 7792

Explanation:

Here we have that the formula for population presented as follows;

`A = P(1+r)^t`

Where:

A = Population after growth

P = Original population = 3400

r = 5% = 0.05

t = Time = 17 years

Population growing at a rate of 5% is thus given by the plugging in the above values into the population growth formula thus;

`A = 3400 * (1+0.05)^(17) = 7792.86`

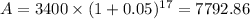
Since we are presenting data relating to number of people, we round alwys down as the statistics should represent the number of whole people on ground.

Therefore, in 17 years time, the initial population of 3400, and growing at a rate of 5% will be ≈ 7792.