Question

A study was conducted to examine the impact of speaking in public on college students. A class of 15 statistics students participated in the study. At the beginning of a lecture,the students recorded their systolic blood pressure. During the lecture the instructor asked each student to stand and answer questions about topics in the lecture. After finishing the speaking,the students once again recorded their blood pressure. The resulting values are given below along with summary statistics.Carry out the appropriate hypothesis test at a significant level α = 0.05.

Before 102 123 128 125 136 108 130 113 105 136 146 138 108 149 132
After 141 142 146 136 144 111 132 114 103 133 140 130 100 133 113
Before-After -39 -19 -18 -11 -8 -3 -2 -1 2 3 6 8 8 16 19
Before After Difference
Mean=125.3 Mean=127.9 Mean=-2.6
StDev=15.03 StDev=15.5 StDev=14.87

Does this information indicate that blood pressure increased because of speaking? Conduct an appropriate hypothesis test and show appropriate steps.

Answer 1

We conclude that the blood pressure has decreased or remained same because of speaking.

Explanation:

We are given that a class of 15 statistics students participated in the study.

The resulting values are given below along with summary statistics;

Before 102 123 128 125 136 108 130 113 105 136 146 138 108 149 132

After 141 142 146 136 144 111 132 114 103 133 140 130 100 133 113

Before-After -39 -19 -18 -11 -8 -3 -2 -1 2 3 6 8 8 16 19

Before After Difference

Mean = 125.3 Mean = 127.9 Mean = -2.6

StDev = 15.03 StDev = 15.5 StDev = 14.87

Let
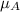`\mu_A` = mean blood pressure of students after speaking.

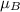`\mu_B` = mean blood pressure of students before speaking.

`\mu_D` =
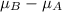`\mu_B-\mu_A` = difference between two mean blood pressures.

So, Null Hypothesis,
`H_0` :
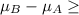`\mu_B-\mu_A \geq` 0 or
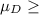`\mu_D\geq` 0 {means that the blood pressure has decreased or remained same because of speaking}

Alternate Hypothesis,
`H_A` :
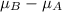`\mu_B-\mu_A` < 0 or
`\mu_D` < 0 {means that the blood pressure has increased because of speaking}

The test statistics that would be used here Paired data t-test statistics;

T.S. =
`(\bar D-\mu_D)/((s_D)/(√(n) ) )` ~
`t_n_-_1`

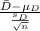where,
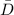`\bar D` = sample mean difference in both blood pressure = -2.6

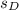`s_D` = sample standard deviation of paired data = 14.87

n = sample of statistics students participated = 15

So, the test statistics =
`(-2.6-0)/((14.87)/(√(15) ) )` ~
`t_1_4`

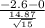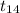
= -0.677

The value of t test statistics is -0.677.

Now, at 0.05 significance level the t table gives critical value of -1.761 at 14 degree of freedom for left-tailed test.

Since our test statistic is more than the critical value of t as -0.677 > -1.761, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that the blood pressure has decreased or remained same because of speaking.