Answer:
1/3
Explanation:
We know that angle subtended by whole circumference is
 .
.
If r is the radius then Length of whole circumference is
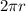
 radian has
radian has
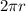 length
length
dividing both side by
 we have
we have
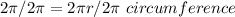
1 radian has r length
1 radian = r length equation a
=> since we have to find value of circumference for
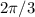 we
we
multiply both side of equation a with
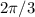 .
.
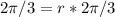
therefore, length of required arc is
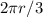
________________________________________________
we have to find how much is this as fraction of total circumference of circle
fraction of circumference = value of arc length / total length of circumference
fraction of circumference =
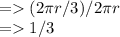
Thus, the given arc is 1/3 of circumference of circle.