Question

Hi guys,

I've got the following problem:

I've tried to apply the chain rule but I just don't get the right answer. Can anyone help me? :)

Answer 1

`\begin{bmatrix}u\\v\end{bmatrix}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x\cos\theta-y\sin\theta\\x\sin\theta+y\cos\theta\end{bmatrix}`

so that

`\begin{cases}u(x,y)=x\cos\theta-y\sin\theta\\v(x,y)=x\sin\theta+y\cos\theta\end{cases}`

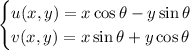
For a function
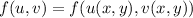`f(u,v)=f(u(x,y),v(x,y))`, we have by the chain rule,

`(\partial f)/(\partial x)=(\partial f)/(\partial u)(\partial u)/(\partial x)+(\partial f)/(\partial v)(\partial v)/(\partial x)`

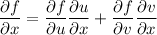
and

`\begin{cases}(\partial u)/(\partial x)=\cos\theta\\\\(\partial v)/(\partial x)=\sin\theta\end{cases}`

`\implies(\partial f)/(\partial x)=\cos\theta(\partial f)/(\partial u)+\sin\theta(\partial f)/(\partial v)`

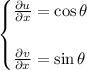
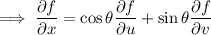
Let
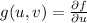`g(u,v)=(\partial f)/(\partial u)` and
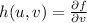`h(u,v)=(\partial f)/(\partial v)`. This substitution is made just to make the application of the chain rule clearer.

`(\partial f)/(\partial x)=\cos\theta\,g+\sin\theta\,h`

Differentiating again wrt
`x` gives

`(\partial^2f)/(\partial x^2)=\cos\theta(\partial g)/(\partial x)+\sin\theta(\partial h)/(\partial x)`

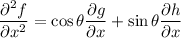
By the chain rule,

`(\partial g)/(\partial x)=(\partial g)/(\partial u)(\partial u)/(\partial x)+(\partial g)/(\partial v)(\partial v)/(\partial x)`

and our substitution shows that, for instance,

`(\partial g)/(\partial u)=(\partial)/(\partial u)(\partial f)/(\partial u)=(\partial^2f)/(\partial u^2)`

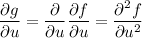
and so

`(\partial g)/(\partial x)=\cos\theta(\partial^2f)/(\partial u^2)+\sin\theta(\partial^2f)/(\partial v\partial u)`

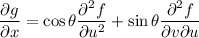
Similarly, we find

`(\partial h)/(\partial x)=\cos\theta(\partial^2f)/(\partial u\partial v)+\sin\theta(\partial^2f)/(\partial v^2)`

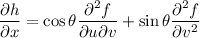
Putting everything together, we have

`(\partial^2f)/(\partial x^2)=\cos^2\theta(\partial^2f)/(\partial u^2)+\cos\theta\sin\theta(\partial^2f)/(\partial v\partial u)+\sin\theta\cos\theta(\partial^2f)/(\partial u\partial v)+\sin^2\theta(\partial^2f)/(\partial v^2)`

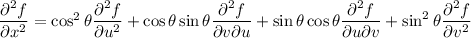
and we can similarly find that

`(\partial^2f)/(\partial y^2)=\sin^2\theta(\partial^2f)/(\partial u^2)-\cos\theta\sin\theta(\partial^2f)/(\partial v\partial u)-\sin\theta\cos\theta(\partial^2f)/(\partial u\partial v)+\cos^2\theta(\partial^2f)/(\partial v^2)`

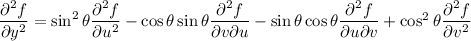
Adding together these derivatives, we see the mixed partials cancel, and recalling that
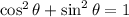`\cos^2\theta+\sin^2\theta=1`, we end up with

`(\partial^2f)/(\partial x^2)+(\partial^2f)/(\partial y^2)=(\partial^2f)/(\partial u^2)+(\partial^2f)/(\partial v^2)`

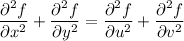
as required.