Answer:
a) Null hypothesis:
H0 : u = 16
b) Alternative hypothesis :
H1 : u < 16
c) Level of significance, a = 10% = 0.10
d) To find the test statistic Z, let's use the formula below:
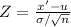
Where,
x' = 15.84
u = 16
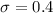
n = 16
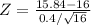
Z = -1.6
This is a left tailed test
Critical value of test statistic at significance level of

f) Decision: reject null hypothesis H0 if Z is less than critical value.
g) From standard normal table, pvalue at Z = - 1.6
Pvalue = 0.0548
Conclusion: Since pvalue,0.0548 is less than significance level of 0.10 and Zo, - 1.6 is less than Zcritical, -1.282 we reject the null hypothesis H0.
Therefore, we conclude that the population mean weight is less than 16oz.