Base 8 to Base 10: Avoiding some headaches
To avoid the hassle of having to learn the base 8 multiplication table, let's convert the number
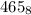 to our more familiar decimal system. The same way each digit in the decimal number 248 represents a multiple of a power of 10, each digit in
to our more familiar decimal system. The same way each digit in the decimal number 248 represents a multiple of a power of 10, each digit in
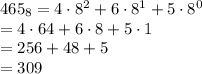
Base 10 to Base 5: Let's regroup
To find the base 5 representation of number, we need to "regroup" these places in terms of powers of 5. That means that every group of 5 1s we can group into 1 5, every group of 5 5s we can group into 1 25, every group of 5 25s we can group into 1 125, and so on. All of the "leftovers" are what give us the digits of our number.
To start converting 309 to base 5, let's figure out how many groups of 5 we have, and how many 1s we have left over.
309 / 5 = 61 R 4, so we can make 61 groups of 5 with 4 1s left over. We're going to put that 4 in the one's place. Now, bundle those 61 groups of 5 in to groups of 5:
61 / 5 = 12 R 1, so we can make 12 groups of 5 5s (or 12 groups of 25) with 1 5 left over. We'll put a 1 in the 5's place and group the 25s together now.
12 / 5 = 2 R 2. That's 2 groups of 5 25s (or 2 groups of 125), and we've got 2 25s left over. That 2's gonna go in the 25's place.
2 / 5 = 0 R 2. Well, we weren't able to bundle those 125s into any larger groups, so all we have left is to put those 2 leftover 125s in the 125s place! We're done with the hard part.
Writing our number out
Now that we've handled the regrouping, let's use those leftovers to put our number together. Let's lay out the digits we have in each of our places:
- 1s place: 4
- 5s place: 1
- 25s place: 2
- 125s place: 2
It's conventional to write numbers in any representation left-to-right from highest place value to lowest, so starting at the 125s place, our base 5 representation will be
2214₅