Question

Suppose the length of each side of a

square is increased by 5 feet. If the
perimeter of the square is now 56 feet,
what were the original side lengths of
the square?

Answer 1

Answer:9 feet

Explanation:

let the original length Of The square be y

When the length is increased by 5,the new length will be y+5

Perimeter=4 x length

Perimeter=56

4 x (y+5)=56

Divide both sides by 4

(4x(y+5))/4=56/4

y+5=14

Collect like terms

y=14-5

y=9

Answer 2

The original side length of the square was 9 ft

Explanation:

Consider that the square was initially of side length "x" (our unknown). Then the sides were all increased by 5 ft, and now the perimeter (addition of all four sides) of the square render 56 ft.

Let's write an equation that represents the addition of the four sides of this new rectangle, and set it equal to 56 ft. Then solve for the unknown "x":

`(x+5)+(x+5)+(x+5)+(x+5)=56\\x+x+x+x+5+5+5+5=56\\4x+20=56\\4x=56-20\\4x=36\\x=9`

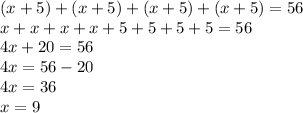
Therefore, the original side of the square was 9 ft.